Option Pricing with Black-Scholes Model & Monte-Carlo method in C++

 
The Black–Scholes or Black–Scholes–Merton model is a mathematical model of a financial market containing derivative investment instruments. From the model, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options. The formula led to a boom in options trading and legitimised scientifically the activities of the Chicago Board Options Exchange and other options markets around the world. lt is widely used, although often with adjustments and corrections, by options market participants. Many empirical tests have shown that the Black–Scholes price is "fairly close" to the observed prices, although there are well-known discrepancies such as the "option smile".
(Source: Wikipedia :https://en.wikipedia.org/wiki/Black%E2%80%93Scholes_model)
 
I believe for anyone who studies math, the BS model is "beautiful"since it provide an explicit solution to a stochastic problem. Here, I am going to implement the Black Scholes model with C++, and show the result and Greeks. For theoratical knowledge of BS, please refer to the link above :).
 
I will also use Monte Carlo Simulation method to price an European option. So, in the main funciton you can see I called both class--BS and MC to achieve the purpose. Ok, here is the code:
 
#0 Main Function:
 
#include<iostream>

#include"mc.h"

#include"bs.h"

using namespace std;

int main()

{

    double underlying = 100.0;

    double strike = 100.0;

    double timeToExpiration = 0.50;

    double riskFreeRate = 0.05;

    double volatility = 0.20;
 
    cout << '\t' << '\t' << " [Black Scholes formula & Monte Carlo Simulation] Program" << endl;

    cout << endl;

    cout << "Basic parameters: " << endl;

    cout << "Strike price: " << strike << endl;

    cout << "Time to experiation: " << timeToExpiration << endl;

    cout << "Risk free rate: " << riskFreeRate << endl;

    cout << "Volatility: " << volatility << endl;

    cout << "~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*~*" << endl;

    Monte_Carlo simu(underlying, strike, riskFreeRate, timeToExpiration, volatility, 50000);

    simu.price();

    BS_Model call_1(underlying,strike,timeToExpiration,riskFreeRate,volatility,"call"  );

    BS_Model put_1(underlying, strike, timeToExpiration, riskFreeRate, volatility, "put");
 
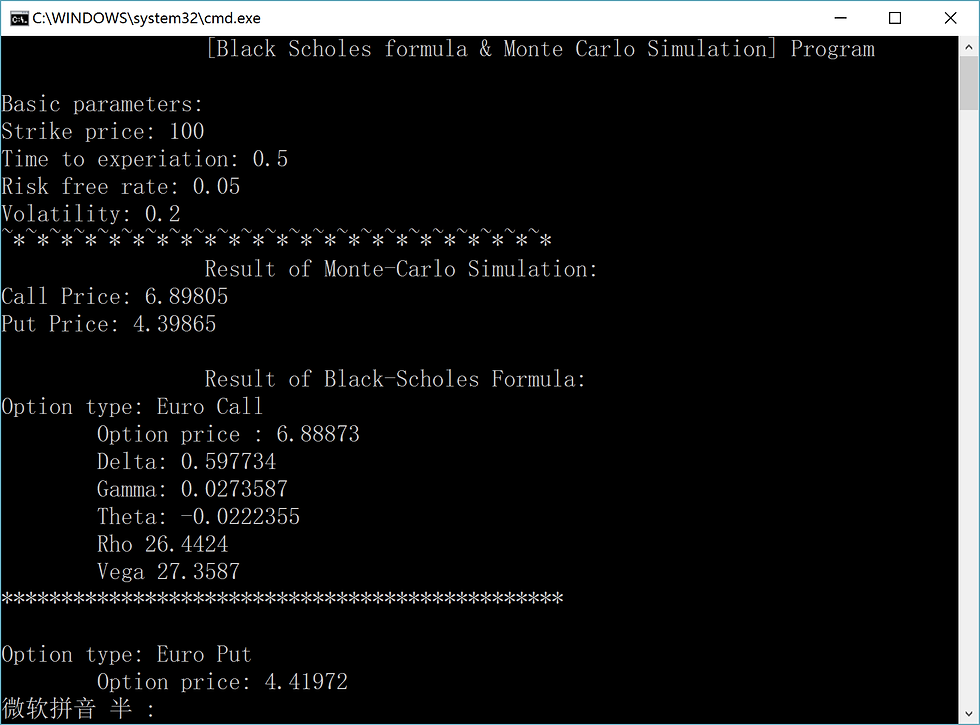
cout << '\t' << '\t' << " Result of Monte-Carlo Simulation:" << endl;

cout << "Call Price: "<<simu.result[0] << endl;

cout << "Put Price: "<<simu.result[1] << endl;

cout << endl;
cout << '\t' << '\t' << " Result of Black-Scholes Formula:" << endl;
cout << "Option type: Euro " << "Call" << endl;

cout << '\t' << "Option price : " << call_1.pricing()<< endl;

cout << '\t' << "Delta: " << call_1.para_delta() << endl;

cout << '\t' << "Gamma: " << call_1.para_gamma() << endl;

cout << '\t' << "Theta: " << call_1.para_theta()/365 << endl;

cout << '\t' << "Rho " << call_1.para_rho() << endl;

cout << '\t' << "Vega " << call_1.para_vega() << endl;

cout << "***********************************************" << endl;

//Put
cout << endl;

cout << "Option type: Euro " << "Put" << endl;

cout << '\t' << "Option price: " << put_1.pricing() << endl;

cout << '\t' << "Delta: " << put_1.para_delta() << endl;

cout << '\t' << "Gamma: " << put_1.para_gamma() << endl;

cout << '\t' << "Theta: " << put_1.para_theta()/365 << endl;

cout << '\t' << "Rho " << put_1.para_rho() << endl;

cout << '\t' << "Vega " << put_1.para_vega() << endl;
cout << endl;

}
 
#1 Header Black Scholes Merton Class:
 
It is clean and easy class. Member functions include the general option pricing function using BS, and Greeks computation function. To price using BS, we should specify the initial underlying asset price, time to maturity, strike price, volatility parameter and the potion type. These parameters are saved as member variables
 
*************************************************************************************************
#ifndef BS_MODEL_H

#define BS_MODEL_H

#include<math.h>

#include<string>

using namespace std;

class BS_Model{
public:

    BS_Model(){};

    BS_Model(double p, double s0, double T, double r, double sigma, string type);

    double standard_N_CDF(double x);

    double pricing();

    double para_delta();

    double para_gamma();

    double para_vega();

    double para_theta();

    double para_rho();

private:

    double underlying_asset_price;

    double strike_price;

    double time_to_exp;

    double risk_free_rate;

    double volatility;

    string option_type;

};

#endif
 
#2 Source file of BS model
Here is how the BS works in C++:
 
Actually, I tried and successed to proof the Black-Scholes Model by hand a few days ago, it cost me some effort, but it is definitely not difficult. As long as we understand the assumption and  idea behind the model, all we need is little patience.
 
Below is simply the implementation of result of BS
 
**********************************************************************************************
 
#include"bs.h"

#include<string>

#include<math.h>

using namespace std;

BS_Model::BS_Model(double p, double s0, double T, double r, double sigma, string type){

    underlying_asset_price = p;

    strike_price = s0;

    time_to_exp = T;

    risk_free_rate = r;

    volatility = sigma;

    option_type = type;

};

double BS_Model::standard_N_CDF(double x){

    double cdf = 0.5*(1 + (erf(x / sqrt(2))));

    return cdf;

}

double BS_Model::pricing(){
    double d1 = (log(underlying_asset_price / strike_price) + time_to_exp*(risk_free_rate + 0.5*volatility*volatility)) / (volatility*sqrt(time_to_exp));

    double d2 = d1 - volatility*sqrt(time_to_exp);

    double price;

    if (option_type == "call")

        price = underlying_asset_price*standard_N_CDF(d1) - exp(-risk_free_rate*time_to_exp)*strike_price*standard_N_CDF(d2);;

    if (option_type == "put")

        price = underlying_asset_price*standard_N_CDF(d1) - exp(-risk_free_rate*time_to_exp)*strike_price*standard_N_CDF(d2) - underlying_asset_price + strike_price*exp(-risk_free_rate*time_to_exp);

    return price;

}

double BS_Model::para_delta(){

    double d1 = (log(underlying_asset_price / strike_price) + time_to_exp*(risk_free_rate + 0.5*volatility*volatility)) / (volatility*sqrt(time_to_exp));

    double delta;

    if (option_type == "call")

        delta = standard_N_CDF(d1);

    else

        delta = standard_N_CDF(d1) - 1;

    return delta;

}

double BS_Model::para_gamma(){

    double d1 = (log(underlying_asset_price / strike_price) + time_to_exp*(risk_free_rate + 0.5*volatility*volatility)) / (volatility*sqrt(time_to_exp));

    double deriv = exp(-d1*d1 / 2.0) / sqrt(2.0*3.14159265359);

    return deriv / underlying_asset_price / volatility / sqrt(time_to_exp);

}

double BS_Model::para_vega(){

    double d1 = (log(underlying_asset_price / strike_price) + time_to_exp*(risk_free_rate + 0.5*volatility*volatility)) / (volatility*sqrt(time_to_exp));

    double deriv = exp(-d1*d1 / 2.0) / sqrt(2.0*3.14159265359);

    return underlying_asset_price*deriv*sqrt(time_to_exp);

}

double BS_Model::para_theta(){
    double d1 = (log(underlying_asset_price / strike_price) + time_to_exp*(risk_free_rate + 0.5*volatility*volatility)) / (volatility*sqrt(time_to_exp));

    double d2 = d1 - volatility*sqrt(time_to_exp);

    double deriv = exp(-d1*d1 / 2.0) / sqrt(2.0*3.14159265359);

    double theta;

    if (option_type == "call")

        theta = -underlying_asset_price*deriv*volatility / 2 / sqrt(time_to_exp) - risk_free_rate*strike_price*exp(-risk_free_rate*time_to_exp)*standard_N_CDF(d2);

    else

        theta = -underlying_asset_price*deriv*volatility / 2 / sqrt(time_to_exp) + risk_free_rate*strike_price*exp(-risk_free_rate*time_to_exp)*standard_N_CDF(-d2);

    return theta;

}

double BS_Model::para_rho(){
    double  d1 = (log(underlying_asset_price / strike_price) + time_to_exp*(risk_free_rate + 0.5*volatility*volatility)) / (volatility*sqrt(time_to_exp));

    double d2 = d1 - volatility*sqrt(time_to_exp);

    double deriv = exp(-d1*d1 / 2.0) / sqrt(2.0*3.14159265359);

    double rho;

    if (option_type == "call")

        rho = time_to_exp*strike_price*exp(-risk_free_rate*time_to_exp)*standard_N_CDF(d2);

    else

        rho = -time_to_exp*strike_price*exp(-risk_free_rate*time_to_exp)*standard_N_CDF(-d2);

    return rho;

}

# Monte Carlo Simulation
 
*********************************************************************************************************
 
#include"mc.h"

Monte_Carlo::Monte_Carlo(double a, double b, double c, double d, double e, double f){

    s0 = a;

    k = b;

    rf = c;

    t = d;

    sigma = e;

    num = f;

}

double Monte_Carlo::normal_factor(){
    static mt19937 superengine;

    normal_distribution<> nor(0.0, 1.0);

    double factor = nor(superengine);

    return factor;

}

void Monte_Carlo:: price(){

    double R = (rf - 0.5*pow(sigma, 2))*t;

    double SD = sigma*sqrt(t);

    double pay_off_c = 0.0;

    double pay_off_p = 0.0;

    for (int i = 1; i <= num; i++)

    {

        double ST = s0*exp(R + SD*normal_factor());

        pay_off_c = pay_off_c + max((ST - k), 0.0);

        pay_off_p = pay_off_p + max((k - ST), 0.0);

    }

    pay_off_c = pay_off_c / num;

    pay_off_p = pay_off_p / num;

    pay_off_c *= exp(-rf*t);

    pay_off_p *= exp(-rf*t);

    result.push_back(pay_off_c);

    result.push_back(pay_off_p);
}
 
# Header of MC
 
#ifndef MONTE_CARLOee_H

#define MONTE_CARLOee_H

#include <chrono>

#include<algorithm>

#include<random>

#include<vector>

using namespace std;
class Monte_Carlo{

public:

    Monte_Carlo(double a, double b, double c, double d, double e, double f);

    double normal_factor();

    void price();

    vector<double>result;
private:

    double s0;

    double k;

    double rf;

    double t;

    double sigma;

    double num;

};

#endif
Harrogath

Option Pricing with Black-Scholes Model & Monte-Carlo method in C++

Who Am I?

Other Posts

Who Am I?

Follow Me
