Monte Carlo Pricing Method of European Call (Python)

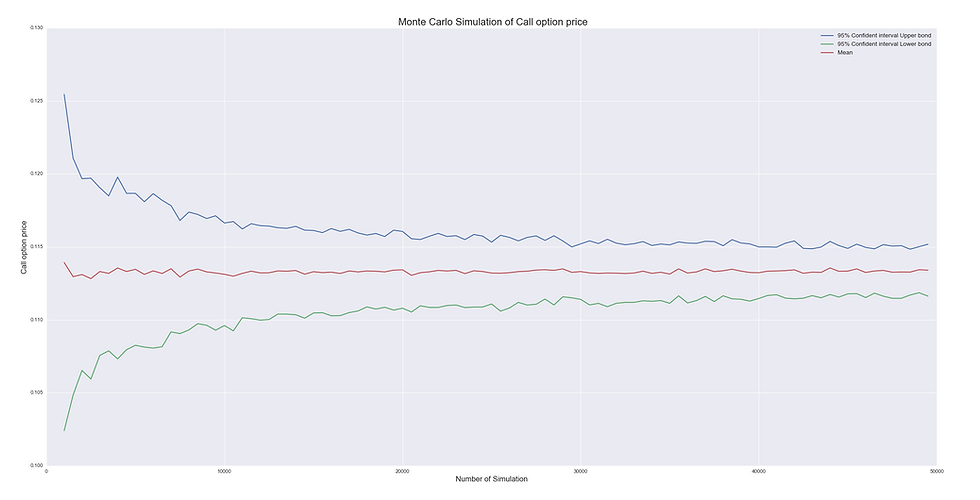
Assuming the underlying stock follows the geometric Brownian process, with some easy Ito calculus, we can actually produce perfect Monte Carlo estimator of the E call option. I omitted the calculus part, since it is trivial. Below is the code and the estimator convergence speed result:
 
*******************************************************************
 
#encoding=utf-8

import numpy as np

import time

from scipy.stats import norm

import matplotlib.pyplot as plt

import seaborn as sns

from math import*
def GORB(a):

    if a<5:

        return "soso"

    else:

        return "too slow!"

#B-S parameters :

S=2.45

K=2.50

t=0.25

r=0.05

sigma=0.25

#

Portfolio=range(0,5000,500)
def BS(S,K,t,r,sigma):

    d1=(log(S/K)+(r+0.5*sqrt(sigma))*t)/(sigma*sqrt(t))

    d2=d1-sigma*sqrt(t)

    return S*norm.cdf(d1)-K*exp(-r*t)*norm.cdf(d2)
def npBS(S,K,t,r,sigma):

    d1=(np.log(S/K)+(r+0.5*sqrt(sigma))*t)/(sigma*sqrt(t))

    d2=d1-sigma*sqrt(t)

    return S*norm.cdf(d1)-K*exp(-r*t)*norm.cdf(d2)

def func1(S,t,r,sigma):

 plt.figure(1)

 sns.set_style("ticks")

 time_series=[]

 for i in Portfolio:

    strike_series=np.linspace(2.0,3.0,i)

    time_now=time.time()

    for x in range(i):

        BS(S,strike_series[x],t,r,sigma)
    time_series.append(time.time()-time_now)
 plt.bar(Portfolio,time_series, color="red",width=200)

 plt.plot()

 plt.show()

 plt.title("Computation running time of option's portfolio-Loop method")

 time_series=np.asarray(time_series)

 print "for loop运行时间（s）:",time_series.sum(),"。。。血崩"

def func2(S,t,r,sigma):

 time_series=[]

 for i in Portfolio:

    strike_series=np.linspace(2.0,3.0,i)

    time_now=time.time()

    npBS(S,strike_series,t,r,sigma)

    time_series.append(time.time()-time_now)
 plt.bar(Portfolio,time_series, color="red",width=200)

 plt.plot()

 plt.title("Computation running time of option's portfolio-Numpy method")

 plt.show()
 time_series=np.asarray(time_series)

 print "vector运行时间（s）:",time_series.sum(),"。。。有点吊"
# func1(S,t,r,sigma)

# func2(S,t,r,sigma)
# Stock price follows geometric brownian motion, pricing call option using monte carlo

def MonteCarlo(S,t,r,sigma,K,path):

  raw_simulators=norm.rvs(size=path,loc=(r-0.5*sigma**2)*t,scale=sigma*sqrt(t))

  raw_simulators=S*np.exp(raw_simulators)

  simulators=np.maximum(raw_simulators-K,0.0).sum()

  price=exp(-r*t)*simulators/path

  return price
# print MonteCarlo(S,t,r,sigma,K,10000)
def MonteCarloConvergenceSpeed(S,t,r,sigma,K):

    size=100

    pathscenario=range(1000,50000,500)

    UpperBond=[]

    LowerBond=[]

    mean=[]

    timemark=time.time()

    for path in pathscenario:

        result=[]

        for simu in range(size):

            result.append(MonteCarlo(S,t,r,sigma,K,path))

        result=np.asarray(result)

        mean.append(result.mean())

        LowerBond.append(result.mean()-1.96*result.std())

        UpperBond.append(result.mean()+1.96*result.std())

    line_table=np.asarray([UpperBond,LowerBond,mean]).T

    plt.plot(pathscenario,line_table)

    plt.title(" Monte Carlo Simulation of Call option price",fontsize=20)

    plt.xlabel("Number of Simulation",fontsize=15)

    plt.ylabel("Call option price",fontsize=15)

    plt.legend(["95% Confident interval Upper bond","95% Confident interval Lower bond","Mean"],fontsize=12)

    timemark=time.time()-timemark
    t=GORB(timemark)

    print "Running Time: ",timemark,t

    plt.show()
MonteCarloConvergenceSpeed(S,t,r,sigma,K)
 
see the result:
Harrogath

Monte Carlo Pricing Method of European Call (Python)

Who Am I?

Other Posts

Who Am I?

Follow Me
